Problem 1
The John Equipment Company estimates its carrying cost at 15% and its ordering cost at $9 per order. The estimated annual requirement is 48,000 units at a price of $4 per unit.
Required:
- What is the most economical number of units to order?
- How many orders should be placed in a year?
- How often should an order be placed?
Solution
1. What is the most economical number of units to order?
Annual requirement = 48,000 units
Ordering cost = $9 per order
Carrying cost = 15% of per-unit cost
Per unit cost = $4 per unit

2. How many orders should be placed in a year?
= Annual requirement / EOQ
= 48,000 units / 1,200 units
= 40 orders
3. How often should an order be placed?
Frequency of orders = No. of days in one year / No. of orders
= 360 days / 40 orders
= 9 days
Problem 2
To date, Raymond Bro. has been purchasing an item in lots of 900 units. This equates to a three-month supply. The cost per unit is $12, the order cost is $16 per order, and the carrying cost is 25%.
Required: How much can Raymond Bro. save per year by purchasing the item in the most economical quantities?
Solution
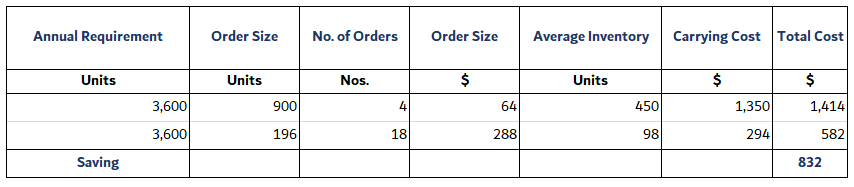
The first stage in our working is to compute the annual requirement.
Given that 900 units amounts to a three-month supply, the monthly requirement is 900 units / 3 months = 300 units.
Therefore, the annual requirement is 300 units x 12 months = 3,600 units.
In turn, the EOQ can be computed as follows:
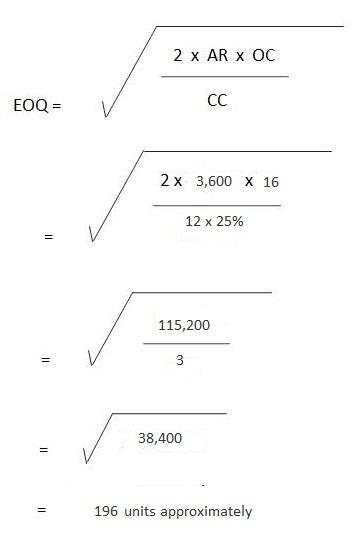
No. of Orders = 3,600 units / 900 units
= 4 orders
= 3,600 units / 196 units
= 18 orders approx.
Ordering Cost = 4 orders x $16 per order
= $64
Also, in the case of EOQ:
= 18 orders x $16 per order
= $288
Average Inventory = 900 units / 2
= 450 units
In the case of EOQ:
= 196 units / 2
= 98 units
Carrying cost = $3 x 450 units
= $1,350
In the case of EOQ:
= $3 x 98 units
= $294
Total cost = $64 + $1,350
$1,414
In the case of EOQ:
=$288 + $294
= $582
Saving = $1,414 - $582
= $832
Problem 3
A manufacturing company places a semi-annual order of 24,000 units at a price of $20 per unit. Its carrying cost is 15% and the order cost is $12 per order.
Required:
- What is the most economical order quantity?
- How many orders need to be placed?
Solution
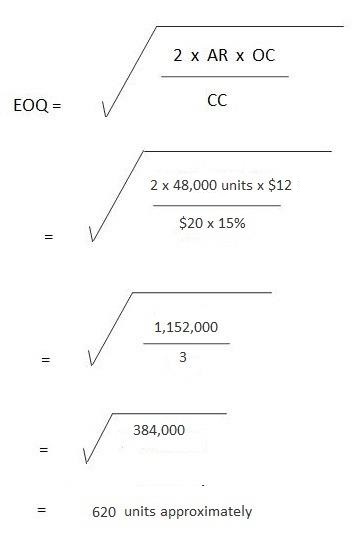
No. of orders per year = Annual Requirement / EOQ
= 48,000 units / 620 units
= 77 orders approximately
To compute the annual requirement:
24,000 units are ordered semiannually, therefore:
Annual requirement = 24,000 units x 2 = 48,000 units.
Economic Order Quantity (EOQ): Practical Problems and Solutions FAQs
EOQ stands for economic order quantity. The formula is: EOQ = √ (2xARxOC) / CC where AR = annual requirements, OC = per unit cost, and CC = carrying cost per unit per year of materials inventory
Efficient means to use the minimum resources to achieve a goal. In this case, it means minimizing your inventory amount. It is helpful because it decreases the money you spend on holding inventory, and lowers the risk of not having enough inventory if a sudden increase was to happen.
Clothing stores order a certain amount in inventory at a time to save on costs. A clothing store, for example, has an EOQ of 10 and sales are going well. If the owner wanted to make more money or generate more sales, they would increase that EOQ amount so they won’t have to keep placing orders as often, saving them time and money in the process.
It minimizes carrying costs and saves time. You can also save a substantial amount of money using this method since you would not have to place as many orders reducing supplier lead time
EOQ does not account for seasonal or economic fluctuations which can cause huge differences in your inventory levels. It does not take into account the random nature of demand.
True Tamplin is a published author, public speaker, CEO of UpDigital, and founder of Finance Strategists.
True is a Certified Educator in Personal Finance (CEPF®), author of The Handy Financial Ratios Guide, a member of the Society for Advancing Business Editing and Writing, contributes to his financial education site, Finance Strategists, and has spoken to various financial communities such as the CFA Institute, as well as university students like his Alma mater, Biola University, where he received a bachelor of science in business and data analytics.
To learn more about True, visit his personal website or view his author profiles on Amazon, Nasdaq and Forbes.











