Convexity measures the curvature of the relationship between bond prices and interest rates. It represents the rate at which the bond's duration changes in response to changes in interest rates. In simple terms, convexity provides a more accurate measure of a bond's price sensitivity to changes in interest rates than duration alone. Understanding convexity is essential for bond investors because it helps them assess the interest rate risk associated with their bond investments. By incorporating convexity into their analysis, investors can better estimate the potential impact of interest rate changes on their bond portfolios and make more informed investment decisions. Duration and convexity are related concepts that help investors measure the price sensitivity of bonds to interest rate fluctuations. While duration provides a linear approximation of a bond's price change in response to changes in interest rates, convexity accounts for the non-linear relationship between bond prices and interest rates, offering a more accurate assessment of price sensitivity. A bond's price is determined by the present value of its future cash flows, which include periodic coupon payments and the principal repayment at maturity. The present value of these cash flows is calculated by discounting them to the present using a discount rate, which is typically the bond's yield to maturity. The yield to maturity (YTM) is the interest rate that equates the present value of a bond's future cash flows to its current price. It represents the total return an investor would earn if they held the bond to maturity and reinvested all coupon payments at the same rate. The YTM is a critical component of bond pricing, as it serves as the discount rate used to calculate the present value of future cash flows. There is an inverse relationship between interest rates and bond prices. When interest rates rise, the present value of a bond's future cash flows decreases, resulting in a lower bond price. Conversely, when interest rates fall, the present value of a bond's future cash flows increases, leading to a higher bond price. The magnitude of the price change in response to interest rate fluctuations depends on the bond's duration and convexity. Bonds with higher duration and convexity tend to experience more significant price changes in response to interest rate shifts. Duration measures a bond's sensitivity to interest rate changes. It represents the weighted average time until a bond's cash flows are received, taking into consideration the present value of each cash flow. The higher the duration, the more sensitive a bond's price is to changes in interest rates. Macaulay duration is the original concept of duration, which measures the weighted average time until a bond's cash flows are received. Modified duration, on the other hand, is an adjusted version of Macaulay duration that directly measures a bond's price sensitivity to changes in interest rates. Duration provides a linear approximation of a bond's price change in response to interest rate changes. However, the relationship between bond prices and interest rates is non-linear, leading to inaccuracies in duration-based price change estimates. This limitation is where convexity comes into play, as it accounts for the non-linear price sensitivity of bonds. Convexity measures the curvature of the relationship between bond prices and interest rates. It is a second-order measure of price sensitivity, providing a more accurate assessment of how a bond's price will change in response to interest rate fluctuations. By considering convexity, investors can better predict the potential impact of interest rate changes on their bond investments. Bonds with positive convexity experience price increases that are larger than the price decreases when interest rates change by equal amounts. This characteristic is desirable for bond investors, as it provides a cushion against interest rate risk. Most regular bonds, such as fixed-rate bonds and zero-coupon bonds, exhibit positive convexity. Bonds with negative convexity have price decreases that are larger than the price increases when interest rates change by equal amounts. This characteristic exposes bond investors to greater interest rate risk. Callable bonds and mortgage-backed bonds typically exhibit negative convexity due to their embedded options, which allow the issuer or borrower to alter the bond's cash flows. Bonds with higher convexity provide a volatility buffer against interest rate changes, as their prices are less sensitive to rate fluctuations. This makes them more attractive to investors seeking to minimize interest rate risk in their bond portfolios. Convexity-adjusted duration combines duration and convexity to accurately measure a bond's price sensitivity to interest rate changes. By incorporating convexity, this metric accounts for the non-linear relationship between bond prices and interest rates, offering a more precise estimate of price changes resulting from rate fluctuations. The formula for convexity is: Where: Σ represents the summation symbol, t is the time period, PV(CF_t) is the present value of the cash flow at time t, P is the bond price, and YTM is the yield to maturity 1. Calculate the present value of each cash flow (coupon payments and principal repayment) using the bond's yield to maturity. 2. Multiply the present value of each cash flow by the corresponding time period squared plus the time period. 3. Sum the results of step 2. 4. Divide the sum by the bond price multiplied by (1 + YTM)^2. Bonds with higher convexity values are less sensitive to interest rate changes, offering lower interest rate risk. Higher convexity indicates that the bond's price will experience smaller fluctuations in response to interest rate shifts, providing a cushion against rate changes. Bonds with lower convexity values are more sensitive to interest rate changes, exposing investors to higher interest rate risk. Lower convexity suggests that the bond's price will experience larger fluctuations in response to interest rate shifts, increasing the potential for losses. Zero-coupon bonds have the highest convexity among fixed-rate bonds, as they do not have periodic coupon payments. Their convexity increases with their time to maturity, making them more sensitive to interest rate changes as their maturity extends. Coupon-paying bonds typically have lower convexity than zero-coupon bonds, as their periodic coupon payments reduce their overall price sensitivity to interest rate changes. The convexity of coupon-paying bonds varies depending on factors such as the coupon rate, time to maturity, and yield to maturity. Callable and putable bonds often exhibit negative convexity due to the embedded options that allow the issuer or bondholder to alter the bond's cash flows. These options can cause bond prices to be more sensitive to interest rate changes in one direction than the other, leading to asymmetric price responses to rate fluctuations. Incorporating convexity into bond portfolio management helps investors diversify their interest rate risk. By selecting bonds with different convexity characteristics, investors can create a bond portfolio with a more balanced exposure to interest rate fluctuations, reducing the potential impact of rate changes on their investments. Active bond portfolio managers can use convexity to capitalize on interest rate trends and market inefficiencies. By monitoring convexity levels across various bonds and adjusting their holdings accordingly, these managers can exploit opportunities to enhance returns and manage risk more effectively. In a rising interest rate environment, bonds with higher convexity are more desirable, as they provide a cushion against the negative impact of rate increases on bond prices. Investing in bonds with higher convexity can help investors mitigate the potential losses associated with rising interest rates. In a falling interest rate environment, bonds with higher convexity can also be beneficial, as they allow investors to capitalize on the positive impact of rate decreases on bond prices. Bonds with higher convexity experience larger price increases in response to falling interest rates, providing the potential for greater capital gains. Understanding convexity is crucial for bond investors, as it offers valuable insights into the interest rate risk associated with their investments. By incorporating convexity into their analysis, investors can better estimate the potential impact of interest rate changes on their bond portfolios and make more informed investment decisions. Convexity serves as an essential tool for risk management and bond portfolio optimization. By considering the convexity characteristics of different bonds, investors can construct portfolios with a more balanced exposure to interest rate risk and enhance their ability to protect against interest rate fluctuations. Furthermore, active bond portfolio managers can use convexity to identify opportunities for capitalizing on interest rate trends and market inefficiencies, potentially generating superior risk-adjusted returns. In order to take advantage of the benefits that convexity can offer in bond investing, it may be worthwhile to consider seeking the guidance of a professional wealth management service. Wealth managers can provide valuable insights and advice on constructing and managing a diversified bond portfolio that considers convexity considerations. What Is Convexity?
Bond Pricing and Convexity
Basics of Bond Pricing
Present Value of Cash Flows
Yield To Maturity
Interest Rate Risk and Bond Prices
Inverse Relationship Between Interest Rates and Bond Prices
Effects of Interest Rate Changes on Bond Prices
Duration as a Measure of Interest Rate Sensitivity
Macaulay Duration and Modified Duration
Limitations of Duration
Convexity as a Measure of Bond Price Sensitivity
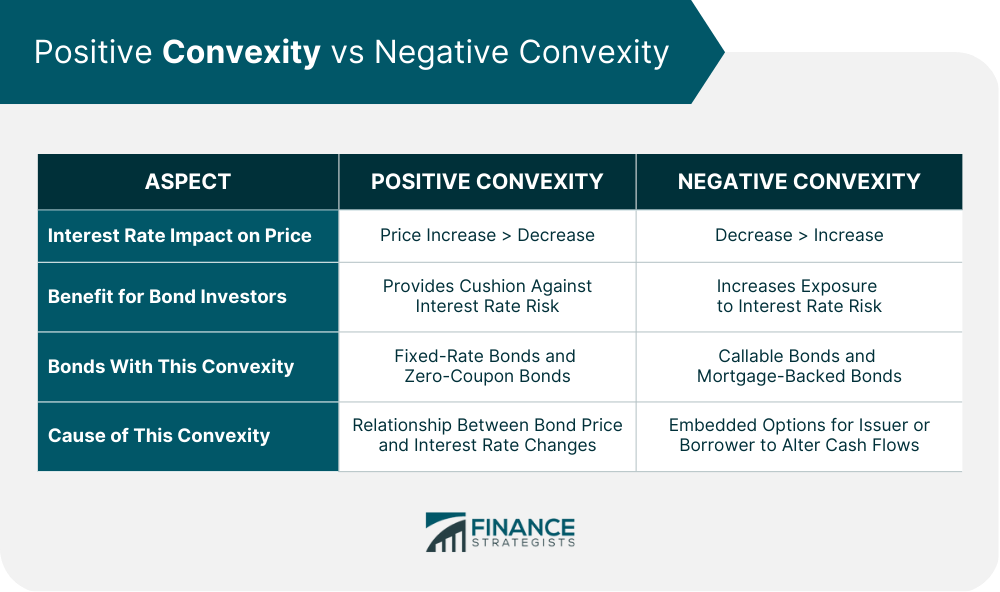
Positive and Negative Convexity
Characteristics of Bonds With Positive Convexity
Characteristics of Bonds With Negative Convexity
Convexity and Bond Price Volatility
Convexity as a Volatility Buffer
Convexity-Adjusted Duration
Measuring Convexity
Formula and Calculation of Convexity

Steps to Calculate Convexity
Interpretation of Convexity Values
Higher Convexity and Lower Interest Rate Risk
Lower Convexity and Higher Interest Rate Risk
Convexity Comparison Across Bonds
Convexity of Zero-Coupon Bonds
Convexity of Coupon-Paying Bonds
Convexity of Callable and Putable Bonds
Convexity in Bond Portfolio Management
Role of Convexity in Managing Bond Portfolios
Diversification of Interest Rate Risk
Active Management and Bond Convexity
Bond Convexity and Market Conditions
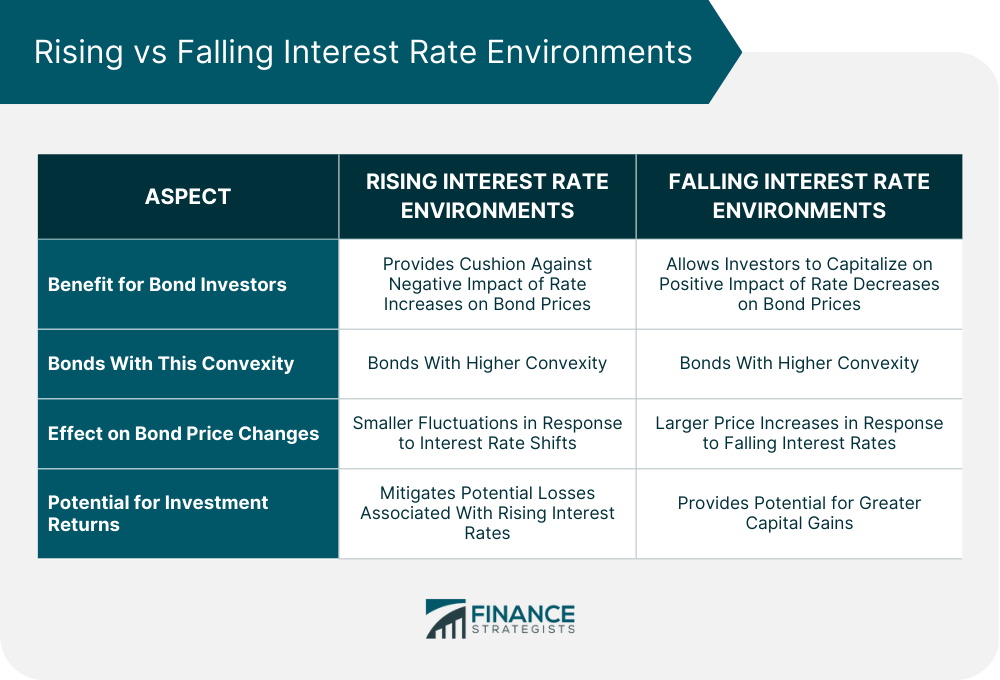
Convexity in Rising Interest Rate Environments
Convexity in Falling Interest Rate Environments
Final Thoughts
Convexity in Bond FAQs
Convexity is a measure of the curvature of the relationship between bond prices and interest rates. It provides a more accurate assessment of a bond's price sensitivity to changes in interest rates than duration alone.
Understanding convexity is crucial for bond investors because it helps them assess the interest rate risk associated with their bond investments. By incorporating convexity into their analysis, investors can better estimate the potential impact of interest rate changes on their bond portfolios and make more informed investment decisions.
Duration and convexity are related concepts that help investors measure the price sensitivity of bonds to interest rate fluctuations. While duration provides a linear approximation of a bond's price change in response to changes in interest rates, convexity accounts for the non-linear relationship between bond prices and interest rates, offering a more accurate assessment of price sensitivity.
The formula for convexity is: Convexity = (Σ [ (t^2 + t) * PV(CF_t) ] ) / (P * (1 + YTM)^2), where Σ represents the summation symbol, t is the time period, PV(CF_t) is the present value of the cash flow at time t, P is the bond price, and YTM is the yield to maturity.
By considering the convexity characteristics of different bonds, investors can construct portfolios with a more balanced exposure to interest rate risk and enhance their ability to protect against interest rate fluctuations. Furthermore, active bond portfolio managers can use convexity to identify opportunities for capitalizing on interest rate trends and market inefficiencies, potentially generating superior risk-adjusted returns.
True Tamplin is a published author, public speaker, CEO of UpDigital, and founder of Finance Strategists.
True is a Certified Educator in Personal Finance (CEPF®), author of The Handy Financial Ratios Guide, a member of the Society for Advancing Business Editing and Writing, contributes to his financial education site, Finance Strategists, and has spoken to various financial communities such as the CFA Institute, as well as university students like his Alma mater, Biola University, where he received a bachelor of science in business and data analytics.
To learn more about True, visit his personal website or view his author profiles on Amazon, Nasdaq and Forbes.