Modified duration is a measure that helps investors assess a bond's interest rate sensitivity. It is a time-weighted measure that estimates the percentage change in a bond's price for a 1% change in yield. This means that the modified duration of a bond can help investors predict how the bond's price will change as interest rates fluctuate. For example, a bond with a modified duration of 5 years would be expected to experience a 5% change in price for a 1% change in yield. If interest rates were to rise by 1%, the price of the bond would be expected to decline by approximately 5%. Conversely, if interest rates were to fall by 1%, the price of the bond would be expected to increase by approximately 5%. The concept of modified duration is an important tool in finance that helps investors manage the risk associated with bond investments. Modified duration helps investors quantify this risk by measuring the sensitivity of a bond's price to changes in interest rates. Investors can use modified duration to adjust the maturity of their bond portfolio in order to better match their risk tolerance and investment objectives. By selecting bonds with different durations, investors can create a portfolio that is more or less sensitive to changes in interest rates, depending on their individual preferences. Modified duration also plays a critical role in evaluating bond performance. By comparing the modified duration of a bond or bond portfolio to its benchmark, investors can assess whether they are achieving their investment objectives. The formula for calculating modified duration is: To illustrate the calculation of modified duration, consider a bond with the following characteristics: Macaulay Duration: 7 years Yield: 6% Coupon Payments per Year: 2 Modified Duration = 7 / (1 + (0.06 / 2)) = 6.60 years The modified duration of a bond is influenced by factors such as time to maturity, coupon rate, yield, and the frequency of coupon payments. The time to maturity of a bond is one of the key factors that affect its modified duration. All other things being equal, a bond with a longer time to maturity will have a higher modified duration than a bond with a shorter time to maturity. This is because longer-term bonds are more sensitive to changes in interest rates than shorter-term bonds. The coupon rate of a bond is another factor that can affect its modified duration. Bonds with higher coupon rates typically have lower modified durations than bonds with lower coupon rates. This is because higher coupon payments reduce the effective duration of a bond, as the bondholder receives more cash flows in the near term. The yield on a bond also affects its modified duration. All other things being equal, a bond with a higher yield will have a lower modified duration than a bond with a lower yield. This is because as yields rise, the price of the bond falls, and the sensitivity of the bond's price to further changes in yield decreases. The frequency of coupon payments is another factor that can affect a bond's modified duration. Bonds that pay coupons more frequently have lower modified durations than bonds that pay coupons less frequently. This is because more frequent coupon payments reduce the effective duration of a bond, as the bondholder receives more cash flows in the near term. Modified duration is used to manage interest rate risk through strategies like portfolio immunization and asset-liability management. These approaches involve matching the modified duration of assets and liabilities to minimize the impact of interest rate changes on the overall portfolio value. Investors employ modified duration in designing bond portfolio strategies, such as active and passive management, duration matching, and convexity optimization. These strategies aim to maximize returns while managing interest rate risk. Modified duration is used to evaluate bond performance by comparing it against benchmarks and conducting attribution analysis. This measure helps investors understand the sources of their portfolio's performance, including the impact of interest rate changes. Modified duration assumes a linear relationship between bond prices and yields, which is only sometimes accurate due to the convex nature of the bond price-yield curve. Convexity, another measure of bond price sensitivity, accounts for this nonlinearity and provides a more accurate estimate of bond price changes for larger yield fluctuations. Modified duration may not be suitable for bonds with embedded options, such as callable and putable bonds. These options can alter the cash flow pattern of a bond, making its price sensitivity to interest rate changes more complex. In such cases, investors should rely on effective duration, which accounts for the potential impact of these options on a bond's price sensitivity. Modified duration is an essential metric in bond investing, as it helps investors assess interest rate risk and manage their bond portfolios effectively. Understanding this measure is crucial for making informed investment decisions and evaluating bond performance. While modified duration has numerous applications in risk management, bond portfolio strategies, and performance evaluation, it also has its limitations. Investors must be aware of its shortcomings when analyzing bonds with nonlinear price-yield relationships or embedded options. In such cases, considering convexity and effective duration can provide a more accurate assessment of interest rate risk. Understanding modified duration and other duration measures is essential for effective risk management in bond investing. By comprehending these measures, investors can better anticipate the impact of interest rate changes on their bond portfolios and employ suitable strategies to manage their exposure to interest rate risk.What Is Modified Duration?
Importance of Modified Duration in Finance
Calculating Modified Duration
Formula

Example
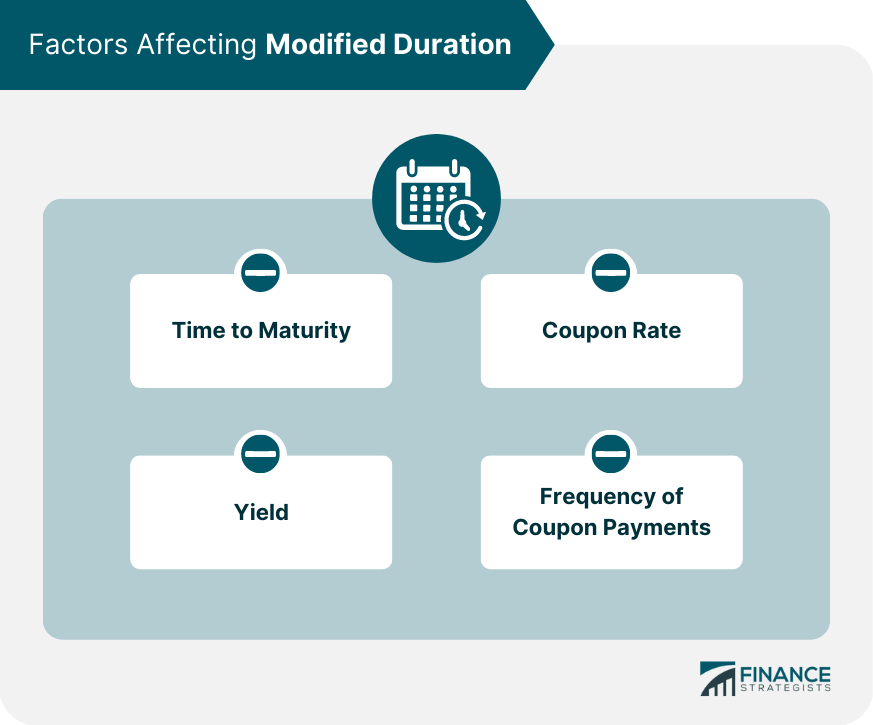
Factors Affecting Modified Duration
Time to Maturity
Coupon Rate
Yield
Frequency of Coupon Payments
Applications of Modified Duration
Managing Interest Rate Risk
Bond Portfolio Strategies
Performance Evaluation

Limitations and Criticisms of Modified Duration
Nonlinear Relationship between Bond Prices and Yields
Applicability to Bonds with Embedded Options
Conclusion
Modified Duration FAQs
Modified duration is a measure of the sensitivity of a bond's price to changes in interest rates, taking into account the bond's cash flows and time to maturity.
Modified duration is calculated as the Macaulay duration divided by (1 + yield to maturity), where the Macaulay duration is the weighted average time until each cash flow from a bond is received.
Modified duration is important for bond investors because it helps them estimate the potential price impact of changes in interest rates on their bond holdings. The higher the modified duration, the more sensitive a bond is to changes in interest rates.
Modified duration and effective duration are both measures of a bond's sensitivity to changes in interest rates, but effective duration takes into account the possibility of changes in cash flows due to prepayments, while modified duration assumes that cash flows remain constant.
Yes, modified duration can be negative for bonds with cash flows that increase as interest rates rise. In this case, the bond's price would actually increase as interest rates rise, and the modified duration would be negative.
True Tamplin is a published author, public speaker, CEO of UpDigital, and founder of Finance Strategists.
True is a Certified Educator in Personal Finance (CEPF®), author of The Handy Financial Ratios Guide, a member of the Society for Advancing Business Editing and Writing, contributes to his financial education site, Finance Strategists, and has spoken to various financial communities such as the CFA Institute, as well as university students like his Alma mater, Biola University, where he received a bachelor of science in business and data analytics.
To learn more about True, visit his personal website or view his author profiles on Amazon, Nasdaq and Forbes.