Portfolio optimization is a critical component of modern finance. At its core, portfolio optimization is the process of constructing an investment portfolio that maximizes returns while minimizing risk. By leveraging a range of quantitative tools and models, portfolio optimization enables investors to achieve diversification, reduce transaction costs, and make informed investment decisions. Modern portfolio theory (MPT) is a widely used method for portfolio optimization. Developed by Harry Markowitz in the 1950s, MPT is based on the idea that investors can achieve the optimal balance of risk and return by diversifying their investments across a range of assets. MPT uses statistical methods to estimate the expected return and risk of different asset classes and securities and then constructs portfolios that maximize returns for a given level of risk. Mean-variance optimization is a method of portfolio optimization that is based on MPT. Mean-variance optimization seeks to construct portfolios that maximize the expected return for a given level of risk. This is done by calculating the expected return and volatility of each asset class or security and using these estimates to construct portfolios that maximize returns while minimizing risk. The Black-Litterman model is a popular method for portfolio optimization that is based on Bayesian statistics. The Black-Litterman model starts with an investor's views on the expected returns of different asset classes or securities and then uses these views to construct portfolios that maximize expected returns while minimizing risk. This model is particularly useful for investors who have strong views on the expected performance of specific asset classes or securities. Monte Carlo simulation is a method of portfolio optimization that uses random sampling to estimate the probability distribution of returns for different asset classes or securities. Monte Carlo simulation can be used to simulate the performance of different investment portfolios over time, which can help investors identify the optimal mix of assets for a given investment objective and risk tolerance. Risk parity is a method of portfolio optimization that seeks to achieve an equal risk contribution from each asset class or security in a portfolio. This is done by allocating investments based on the volatility or risk of each asset class or security, rather than the expected return. By using risk parity, investors can achieve a more balanced and stable investment portfolio. One of the most important factors affecting portfolio optimization is risk tolerance. Investors with a high risk tolerance may be more willing to accept higher levels of risk in exchange for potentially higher returns, while investors with a lower risk tolerance may be more focused on achieving stable and predictable returns. The investment time horizon is another important factor that can affect portfolio optimization. Investors with a longer investment time horizon may be able to take on more risk in their portfolios, while investors with a shorter time horizon may be more focused on preserving capital and achieving steady returns. Market conditions, such as changes in interest rates, inflation, or economic growth, can have a significant impact on portfolio optimization. Investors must stay up-to-date on market conditions and adjust their portfolios accordingly to ensure that they are taking advantage of opportunities and minimizing risks. The selection of asset classes is a critical factor in portfolio optimization. Different asset classes, such as stocks, bonds, and commodities, have different risk and return characteristics. Investors must carefully consider the expected returns and risks of each asset class and construct portfolios that balance these characteristics appropriately. The correlation and covariance between different asset classes or securities is another important factor that can affect portfolio optimization. Assets that are highly correlated may not provide the same diversification benefits as assets that are uncorrelated or negatively correlated. By understanding the correlation and covariance between different assets, investors can construct portfolios that maximize diversification and minimize risk. Excel Solver is a popular tool for portfolio optimization. Excel Solver is an add-in for Microsoft Excel that can be used to solve complex optimization problems, including portfolio optimization. By entering a set of constraints and objectives, Excel Solver can be used to find the optimal mix of assets for a given investment objective and risk tolerance. The portfolio optimization software is another option for investors who are looking to optimize their portfolios. Portfolio optimization software uses sophisticated algorithms and models to identify the optimal mix of assets for a given investment objective and risk tolerance. These programs can be customized to include different asset classes and securities and can provide detailed reports on expected returns and risks. Algorithmic trading platforms are another option for investors who are looking to optimize their portfolios. Algorithmic trading platforms use computer algorithms to analyze market data and identify investment opportunities. These platforms can be used to construct portfolios that are optimized for a given investment objective and risk tolerance. Robo-advisors are online investment platforms that use algorithms to construct and manage investment portfolios. Robo-advisors are designed to provide low-cost, automated portfolio management services to investors. These platforms can be customized to include different asset classes and securities and can be optimized for a range of investment objectives and risk tolerances. Portfolio optimization enables investors to maximize returns by constructing portfolios that are tailored to their specific investment objectives and risk tolerance. By diversifying across asset classes and securities, investors can capture a broad range of returns while minimizing the impact of individual asset performance. In addition to maximizing returns, portfolio optimization also helps investors minimize risk by diversifying across asset classes and securities. By spreading investments across multiple securities, investors can reduce their exposure to individual security risk and achieve a more stable and predictable investment return. Portfolio optimization also enables investors to achieve diversification, which is the process of spreading investments across different asset classes and securities to reduce risk. By diversifying investments, investors can benefit from the return potential of different asset classes while reducing the overall risk of their portfolio. Finally, portfolio optimization can also help investors reduce transaction costs, which are the fees and expenses associated with buying and selling securities. By optimizing portfolio construction, investors can reduce the number of transactions required to achieve their investment objectives, which can lead to lower transaction costs. One of the biggest challenges in portfolio optimization is the quality and availability of data. Investors must have access to reliable and accurate data on different asset classes and securities in order to make informed investment decisions. Portfolio optimization models are based on a range of assumptions and limitations, which can affect the accuracy and reliability of their output. Investors must be aware of these assumptions and limitations and must carefully consider their implications when constructing investment portfolios. Market conditions can change rapidly and unpredictably, which can have a significant impact on portfolio optimization. Investors must be able to quickly adapt to changing market conditions and adjust their portfolios accordingly. Investors may also be subject to a range of behavioral biases that can affect their investment decisions. These biases, such as loss aversion and overconfidence, can lead to suboptimal investment decisions and can negatively impact portfolio optimization. Asset allocation is one of the most common applications of portfolio optimization. Asset allocation involves dividing an investment portfolio among different asset classes, such as stocks, bonds, and commodities, to achieve a balance between risk and return. By using portfolio optimization techniques, investors can construct portfolios that are optimized for a given investment objective and risk tolerance. Risk management is another important application of portfolio optimization. By using portfolio optimization techniques, investors can identify and manage risks in their portfolios. This can involve diversifying across different asset classes and securities, or using hedging strategies to protect against specific risks. Portfolio optimization can also be used for performance evaluation. By comparing the actual performance of a portfolio to its expected performance, investors can identify areas where the portfolio may be underperforming and make adjustments accordingly. Portfolio rebalancing is the process of adjusting the composition of a portfolio to bring it back in line with the investor's target asset allocation. By using portfolio optimization techniques, investors can identify when and how to rebalance their portfolios to maintain a balance between risk and return. Portfolio optimization is a critical component of modern finance. By using a range of quantitative tools and models, portfolio optimization enables investors to construct portfolios that maximize returns while minimizing risk. Portfolio optimization can be used for a range of applications, including asset allocation, risk management, performance evaluation, and portfolio rebalancing. While there are challenges to portfolio optimization, such as data quality and availability and model assumptions and limitations, the benefits of portfolio optimization make it an essential tool for investors who are looking to achieve financial success.Definition Portfolio Optimization
Portfolio Optimization Methods

Modern Portfolio Theory
Mean-Variance Optimization
Black-Litterman Model
Monte Carlo Simulation
Risk Parity
Factors Affecting Portfolio Optimization
Risk Tolerance
Investment Time Horizon
Market Conditions
Asset Class Selection
Correlation and Covariance
Portfolio Optimization Tools and Software
Excel Solver
Portfolio Optimization Software
Algorithmic Trading Platforms
Robo-Advisors
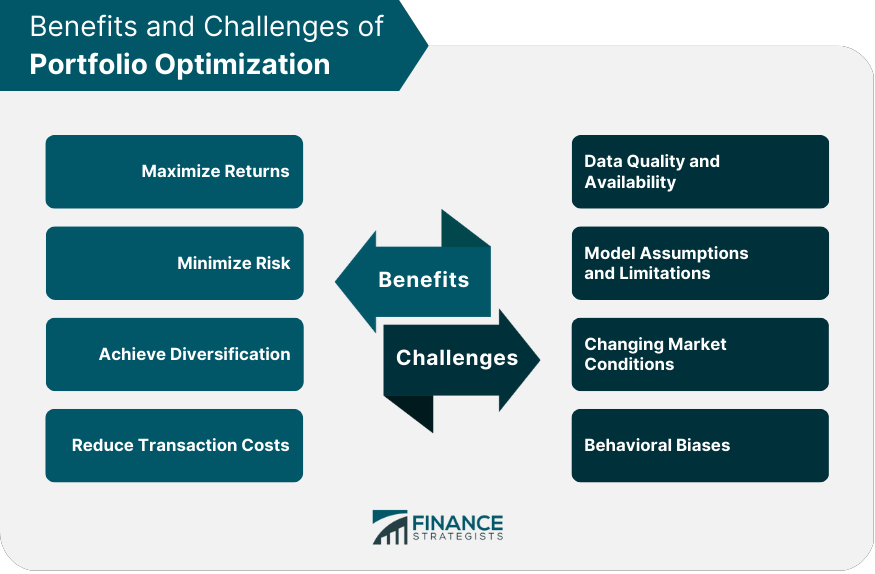
Benefits of Portfolio Optimization
Maximizing Returns
Minimizing Risk
Achieving Diversification
Reducing Transaction Costs
Challenges in Portfolio Optimization
Data Quality and Availability
Model Assumptions and Limitations
Changing Market Conditions
Behavioral Biases
Applications of Portfolio Optimization
Asset Allocation
Risk Management
Performance Evaluation
Portfolio Rebalancing
Conclusion
Portfolio Optimization FAQs
Portfolio optimization is the process of constructing an investment portfolio that maximizes returns while minimizing risk.
The benefits of portfolio optimization include maximizing returns, minimizing risk, achieving diversification, and reducing transaction costs.
Common methods used in portfolio optimization include modern portfolio theory, mean-variance optimization, the Black-Litterman model, Monte Carlo simulation, and risk parity.
Factors that can affect portfolio optimization include risk tolerance, investment time horizon, market conditions, asset class selection, and correlation and covariance.
Portfolio optimization can be used for asset allocation, risk management, performance evaluation, and portfolio rebalancing.
True Tamplin is a published author, public speaker, CEO of UpDigital, and founder of Finance Strategists.
True is a Certified Educator in Personal Finance (CEPF®), author of The Handy Financial Ratios Guide, a member of the Society for Advancing Business Editing and Writing, contributes to his financial education site, Finance Strategists, and has spoken to various financial communities such as the CFA Institute, as well as university students like his Alma mater, Biola University, where he received a bachelor of science in business and data analytics.
To learn more about True, visit his personal website or view his author profiles on Amazon, Nasdaq and Forbes.