Value at Risk is a widely used risk measure that estimates the potential loss in the value of a portfolio or financial instrument over a specific time horizon and with a given level of confidence. It quantifies the maximum potential loss an investor could experience in a specified period under normal market conditions. VaR is an essential tool in risk management, as it helps investors and financial institutions assess and quantify the risk associated with their investment portfolios. By understanding the potential losses that could occur, decision-makers can implement appropriate strategies to mitigate risks and optimize returns. VaR has numerous applications in finance, including portfolio management, risk budgeting, performance evaluation, regulatory compliance, and stress testing. It is widely used by banks, investment firms, hedge funds, and other financial institutions to manage and control their exposure to market risks. The time horizon is a critical component of VaR calculation, as it represents the period over which potential losses are estimated. A longer time horizon typically results in higher VaR estimates, as the probability of larger losses increases over time. The confidence level indicates the probability that the estimated VaR will not be exceeded during the specified time horizon. Commonly used confidence levels are 95% or 99%, meaning that there is a 5% or 1% chance, respectively, that losses will exceed the calculated VaR. Loss distribution is the statistical representation of potential losses within the specified time horizon and confidence level. VaR calculations often assume a normal distribution of returns, although alternative distributions can be used to account for non-normal or skewed return patterns. The parametric method, also known as the variance-covariance method, is a widely used VaR calculation approach that assumes normally distributed returns and relies on the mean and standard deviation of returns to estimate potential losses. This method is computationally efficient but relies on strong assumptions about the distribution of returns. The historical simulation method calculates VaR by analyzing past market data to simulate potential future losses. This non-parametric approach does not require assumptions about the distribution of returns but may not accurately capture potential future losses in the presence of significant market changes. The Monte Carlo simulation method estimates VaR by generating a large number of random scenarios based on historical data and statistical models. This approach accounts for non-linear relationships and non-normal return distributions, but it can be computationally intensive and requires robust model assumptions. A common limitation of VaR calculations is the assumption of normally distributed returns, which may not accurately reflect the actual distribution of financial returns. This assumption can underestimate the risk of extreme events and lead to incorrect VaR estimates. Another simplification in VaR calculations is the assumption of constant volatility, which may not accurately capture the dynamic nature of financial markets. Changes in market conditions and volatility can significantly impact the accuracy of VaR estimates. VaR does not adequately account for tail risk or extreme events, as it focuses on potential losses within a specified confidence level. This limitation can lead to underestimation of the true risk exposure, particularly during periods of market turbulence or financial crises. Comparability and aggregation issues can arise when comparing or combining VaR estimates across different assets, portfolios, or time horizons. Inconsistent calculation methods, assumptions, or data inputs can lead to misleading comparisons and incorrect conclusions about risk exposures. Standardizing VaR calculations and reporting can help mitigate these challenges. Conditional Value at Risk, also known as Expected Shortfall, is an alternative risk measure that addresses some of VaR's limitations by focusing on the expected loss beyond the VaR threshold. CVaR provides a more comprehensive view of tail risk, as it considers the magnitude of losses in extreme events, rather than simply estimating the maximum loss within a given confidence level. Stress testing is a risk management tool that evaluates the potential impact of extreme market events or scenarios on a portfolio. Unlike VaR, stress testing does not rely on historical data or specific probability distributions, allowing for a more flexible and comprehensive assessment of risk exposure under various adverse conditions. Scenario analysis is another alternative to VaR, focusing on the potential impact of specific market events or changes on a portfolio's value. By analyzing a portfolio's sensitivity to various scenarios, investors can better understand their exposure to different risks and take appropriate actions to manage those risks. RiskMetrics and other risk measures, such as the Sharpe or Sortino ratios, offer additional ways to assess and manage portfolio risk. These measures can provide insights into the risk-adjusted performance of a portfolio, complementing VaR calculations and addressing some of their limitations. Incorporating VaR into portfolio construction and diversification strategies can help investors manage risk more effectively. By understanding the VaR of individual assets and the overall portfolio, investors can optimize asset allocation and reduce the potential for large losses. Risk budgeting and allocation involve setting a target level of risk for a portfolio and allocating capital accordingly. By using VaR as a guide, investors can ensure that their portfolios remain within their desired risk tolerance, helping to achieve more consistent returns and manage potential losses. Regular monitoring and reporting of VaR are essential for effective risk management. By tracking changes in VaR over time, investors can identify emerging risks, assess the effectiveness of their risk management strategies, and make informed decisions about adjusting their portfolios. Understanding VaR is crucial for investors and financial institutions seeking to manage risk effectively. By providing a quantitative estimate of potential losses, VaR enables decision-makers to implement appropriate strategies to mitigate risk and optimize returns. Balancing VaR and investment performance are essential for achieving long-term financial success. While minimizing VaR can reduce potential losses, it may also limit upside potential. Investors should carefully consider their risk tolerance and investment objectives when making portfolio allocation and risk management decisions. Managing VaR effectively in portfolio management involves combining techniques, including portfolio diversification, risk budgeting, regular monitoring, and reporting. By adopting these best practices, investors can better manage their risk exposure and achieve more consistent investment performance. To effectively manage VaR and optimize your investment performance, consider seeking the assistance of professional wealth management services. What Is Value at Risk (VaR)?
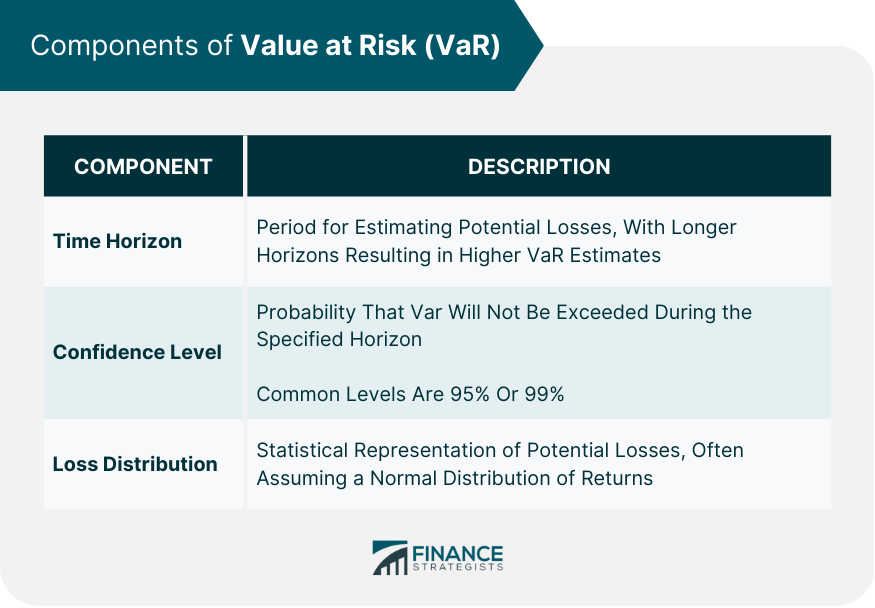
Components of VaR
Time Horizon
Confidence Level
Loss Distribution
Methods for Calculating VaR
Parametric (Variance-Covariance) Method
Historical Simulation Method
Monte Carlo Simulation Method

Limitations of Value at Risk
Assumptions and Simplifications
Normal Distribution
Constant Volatility
Tail Risk and Extreme Events
Comparability and Aggregation Issues
Extensions and Alternatives to VaR
Conditional Value at Risk (CVaR)
Stress Testing
Scenario Analysis
RiskMetrics and Other Risk Measures

Implementing Value at Risk in Portfolio Management
Portfolio Construction and Diversification
Risk Budgeting and Allocation
Monitoring and Reporting VaR
Final Thoughts
Value at Risk (VaR) FAQs
Value at Risk (VaR) is a risk measure that estimates the potential loss in the value of a portfolio or financial instrument over a specific time horizon and with a given level of confidence.
There are several methods for calculating VaR, including the parametric (variance-covariance) method, the historical simulation method, and the Monte Carlo simulation method. Each method has its advantages and limitations.
VaR has several limitations, such as the assumption of normally distributed returns, constant volatility, and the inability to capture tail risk or extreme events adequately.
Alternatives to VaR include Conditional Value at Risk (CVaR), stress testing, scenario analysis, and other risk measures such as the Sharpe ratio or the Sortino ratio.
VaR can be used in portfolio management for portfolio construction and diversification, risk budgeting and allocation, and regular monitoring and reporting of risk exposures.
True Tamplin is a published author, public speaker, CEO of UpDigital, and founder of Finance Strategists.
True is a Certified Educator in Personal Finance (CEPF®), author of The Handy Financial Ratios Guide, a member of the Society for Advancing Business Editing and Writing, contributes to his financial education site, Finance Strategists, and has spoken to various financial communities such as the CFA Institute, as well as university students like his Alma mater, Biola University, where he received a bachelor of science in business and data analytics.
To learn more about True, visit his personal website or view his author profiles on Amazon, Nasdaq and Forbes.